Sei uno di quelli che pensa che le corde della chitarra classica abbiano tutte la stessa tensione?

Contrariamente a quanto possa sembrare  le montature per chitarra classica  non seguono affatto un eguale profilo di tensione tra le corde.

In questo grafico riportiamo ad esempio la tensione di lavoro di alcuni set di corda di differenti aziende:

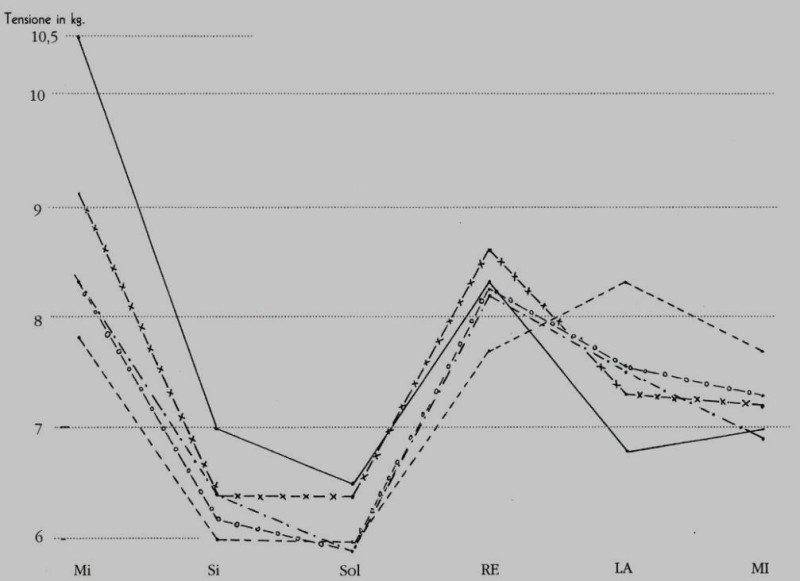
Profilo di tensione delle sei corde in cinque differenti marche

Perché?

Il metodo più comune di valutazione del grado di tensione delle corde di una chitarra è quello di premerle con le dita della mano destra vicino al ponte:  una montatura viene giudicata  ben fatta quando tutte le corde oppongono la stessa forza di contrasto al dito premente.  Verrebbe pertanto da concludere che sono state  tutte calcolate con la stessa tensione di lavoro.

Ma questo tipo di valutazione è in realtà una ‘sensazione tattile’ della tensione, non la tensione in Kg o libbre  propriamente detta misurabile con strumenti adatti. Per una legge della Fisica,  due corde che producono la stessa quantità di spostamento laterale a parità di peso agente e di punto dove si esercita l’applicazione della forza  (che è in pratica il dito che preme)  hanno anche la stessa tensione in Kg.  Ma questa egualità della tensione non corrisponde però quella che viene impostata nel calcolo necessario per determinare i diametri di corda.

Il perché è semplice: in stato di trazione le corde si allungano (questo si evidenzia in particolare nei giri impartiti alla corda in fase di accordatura); questo comporta  di conseguenza anche una  progressiva  riduzione del diametro. Ma se il diametro si riduce anche la tensione di lavoro  ne subirà un calo proporzionale rispetto a quella originaria determinata per calcolo. La quantità di allungamento non è la stessa per tutte le corde; essa risulta  massima  per il cantino, un po’ meno per la seconda corda e molto meno per la terza:  è noto infatti a tutti che i giri di meccanica da fornire al cantino sono molto più numerosi di quelli necessari alla terza corda. Di conseguenza una montatura che fosse stata calcolata in eguale tensione una volta posta in stato di intonazione diventerebbe completamente sbilanciata.

Questo fatto è inevitabile: una chitarra infatti non solo monta corde di natura fisica eterogenea (le prime tre sono in monofilamento sintetico; i bassi invece sono composti da due materiali tra loro accoppiati come bava sintetica e filo metallico di ricopertura)  ma anche di diametro diverso ed occupanti nello  strumento una posizione specifica che viene definita dai tecnici  ‘Indice di Lavoro’ (che è il prodotto tra la frequenza della corda e la lunghezza vibrante). Tutto questo fa sì che il raggiungimento di una omogenea tensione tattile tra le corde sia  nella  realtà un fatto complesso rispetto al semplice calcolo teorico dove il parametro tensione viene posto  come costante.

La scalarità della tensione è quindi  un processo di compensazione  studiata con cura dal cordaio al fine di neutralizzare, corda per corda, la perdita di diametro causata dall’allungamento in trazione: una volta poste in stato stabile di intonazione ciascuna di esse si ridurrà percentualmente del suo valore sino ad assumere  una tensione di lavoro eguale alle altre. Si realizzerà pertanto la condizione in cui, premute con un dito, esse manifesteranno  la stessa flessione. In termini pratici se il cantino cala sperimentalmente del 2% allora nel calcolo di partenza il diametro andrà  maggiorato del 2% e così via con tutte le altre corde.

Ma nella realtà pratica la pendenza del profilo di tensione deve essere reso ancora più accentuato: lo scopo di questa esasperazione della scalarità della tensione di lavoro  è finalizzata a  contrastare con maggior efficacia  la crescita di frequenza delle  corde  di maggior diametro (seconda  ed in particolare la terza)  sui tasti acuti e sopracuti.  Con le montature di budello del passato una ulteriore accentuazione della scalarità della tensione  rispetto a quella necessaria a compensare la perdita di diametro non si rendeva necessaria poiché  le corde di più grossa sezione venivano automaticamente realizzate con maggior torsione (sono quindi più elastiche) mentre i monofilamenti  di materia plastica  presentano tutti il medesimo coefficiente di allungamento specifico.  Il provvedimento  – con le corde sintetiche- non si è rivelato però del tutto sufficiente;  si rende infatti spesso  ancora necessario una serie di interventi di tipo compensatorio  all’osso del ponticello di cui il più comune l’inclinazione dello stesso.

per maggiori approfondimenti andare qui

Mimmo Peruffo 2010